Priority Queue & Heap

Priority queue is a very useful data structure. It can provide the maximum or minimum value in constant time. Before understanding it, we need to understand another data structure called heap because priority queue is often implemented with heap.

Heap

Heap data structure is an array, we can view it as a complete binary tree. We use A[1:n] to represent the array of heap, so A is an array of size n. The index of A starts from 1. A.heapSize means that there are heapSize elements stored in A, so . The figure below shows a max-heap represented as a tree and how its elements are stored in an array.

Because the heap is actually an array, but we will treat it as a complete binary tree. Therefore, for a node i that is index i, we often need to obtain its parent, left child, and right child.

Parent(i) {
    return floor(i / 2)
}

Left(i) {
    return 2 * i
}

Right(i) {
    return 2 * i + 1
}

Heap Property

There are two types of Heap, one is max-heap and the other is min-heap. The property of Max-heap is that for each node i, its value is greater than the values ​​of all nodes in its subtree. On the contrary, the property of min-heap is that for each node i, its value is smaller than the values ​​of all nodes in its subtree. Therefore, the root of max-heap is the maximum value; and the root of min-heap is the minimum value.

Maintaining Heap Property

A heap must satisfy its property. When a heap violates its property, we need a procedure to make the heap satisfy its property. We can use the following MaxHeapify to make a subtree satisfy the max-heap property.

The input of MaxHeapify is the array and index i of a heap. It can make node i and its subtrees satisfy the max-heap property if node i violates the max-heap property. MaxHeapify compares node i with its left and right children, swaps node i with the largest child, and then recursively does the same for the swapped children. The time complexity of MaxHeapify is , where h is the height of the tree.

Algorithm MaxHeapify(A, i) {
    left := Left(i)
    right := Right(i)

    if left <= A.heapSize && A[left] > A[i] {
        largest := left
    } else {
        largest := i
    }

    if right <= A.heapSize && A[right] > A[largest] {
        largest := right
    }

    if largest != i {
        swap(A[i], A[largest])
        MaxHeapify(A, largest)
    }
}

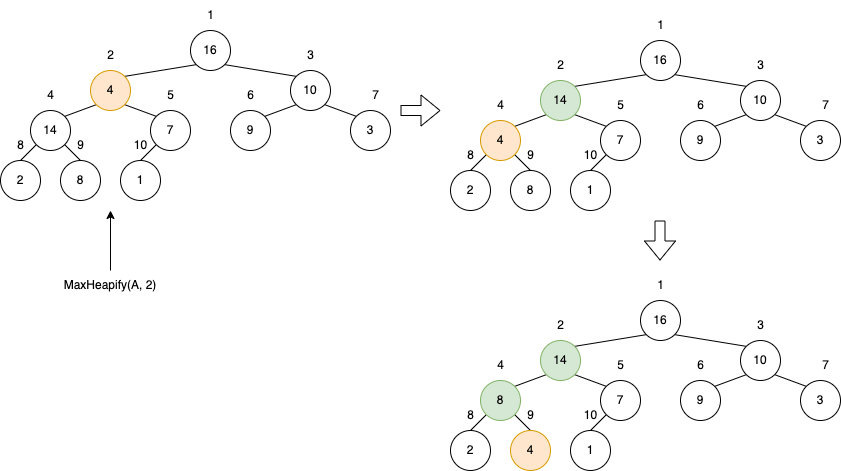
The following example is to do MaxHeapify(A, 2) on the node at index 2.

Building a Heap

The following algorithm BuildMaxHeap converts an array A[1:n] into a max-heap. Its time complexity is .

Algorithm BuildMaxHeap(A, n) {
    A.heapSize := n
    for i := floor(n / 2) to 1 {
        MaxHeapify(A, i)
    }
}

Priority Queue

Priority queue is a data structure and maintains a set S of elements. There are two types of priority queues, one is max-priority queue and the other is min-priority queue. A max-priority queue provides the following operations:

• Max(S): returns the maximum value in S.
• ExtractMax(S): Remove and return the maximum value in S.
• Insert(S, x): Add x to S.

Because of Max(S) and ExtractMax(S) of max-priority queue, we can use max-heap to implement max-priority queue. The following is the max-priority queue algorithm, where A represents the array of max-heap. Additionally, their time complexities are as follows:

• Max(A):
• ExtractMax(A):
• Insert(A, x):

Algorithm Max(A) {
    if A.heapSize < 1 {
        error "heap underflow"
    }
    return A[1]
}

Algorithm ExtractMax(A) {
    max := Maximum(A)
    A[1] := A[A.heapSize]
    A.heapSize := A.heapSize - 1
    MaxHeapify(A, 1)
    return max
}

Algorithm Insert(A, x) {
    if A.heapSize == A.size {
        error "A has no room for x"
    }
    A.heapSize := A.heapSize + 1
    A[A.heapSize] = x
    i := A.heapSize
    while i > 1 && a[Parent(i)] < x {
        swap(A[i], A[Parent(i)])
        i := Parent(i)
    }
}

參考

• Ellis Horowitz, Sartaj Sahni, Sanguthevar Rajasekaran, Computer Algorithm.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, Introduction to Algorithms, 4th Ed.