Problem
You are given an array of words where each word consists of lowercase English letters.
wordA is a predecessor of wordB if and only if we can insert exactly one letter anywhere in wordA without changing the order of the other characters to make it equal to wordB.
For example, "abc" is a predecessor of "abac", while "cba" is not a predecessor of "bcad".
A word chain is a sequence of words [word1, word2, ..., wordk] with k >= 1, where word1 is a predecessor of word2, word2 is a predecessor of word3, and so on. A single word is trivially a word chain with k == 1.
Return the length of the longest possible word chain with words chosen from the given list of words.
Example 1:
Input: words = ["a","b","ba","bca","bda","bdca"] Output: 4 Explanation: One of the longest word chains is ["a","ba","bda","bdca"].
Example 2:
Input: words = ["xbc","pcxbcf","xb","cxbc","pcxbc"] Output: 5 Explanation: All the words can be put in a word chain ["xb", "xbc", "cxbc", "pcxbc", "pcxbcf"].
Example 3:
Input: words = ["abcd","dbqca"] Output: 1 Explanation: The trivial word chain ["abcd"] is one of the longest word chains. ["abcd","dbqca"] is not a valid word chain because the ordering of the letters is changed.
Solution
In this problem, wordA is a predecessor of wordB which means we only need to insert a letter in wordA to make it the same as wordB. However, to insert a letter into a place, we need to consider 26 letters. This increases the overall complexity. If we think about it the other way around, remove a letter from it , and check if there are other words that are the same as it. In this case, the overall complexity is reduced a lot.
In the following example, assume we check bdca and remove the first letter to become dca, which is not the same as the other words. Then, remove the second letter to become bca, and there is bca in words. Recursively do the same for bca.
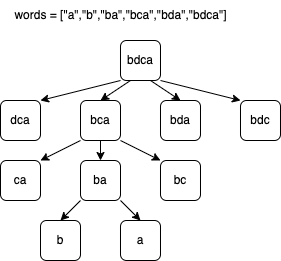
Dynamic Programming
- Time:
- Space:
class Solution {
public int longestStrChain(String[] words) {
Map<String, Integer> dp = new HashMap<>();
for (String word : words) {
dp.put(word, null);
}
int longest = 0;
for (String word : words) {
longest = Math.max(longest, longestStrChain(word, dp));
}
return longest;
}
private int longestStrChain(String word, Map<String, Integer> dp) {
if (word.length() == 0) return 0;
if (!dp.containsKey(word)) return 0;
if (dp.get(word) != null) return dp.get(word);
int longest = 0;
for (int i = 0; i < word.length(); i++) {
String predecessor = word.substring(0, i) + word.substring(i + 1);
longest = Math.max(longest, 1 + longestStrChain(predecessor, dp));
}
dp.put(word, longest);
return longest;
}
}參考
- 1048. Longest String Chain, LeetCode.
- 1048. Longest String Chain, LeetCode Solutions.










