卡方檢定(Chi-Square Test)根據觀察次數(observed frequencies)測定在交叉表裡的變數是否有無關聯。SciPy 的 chi2_contingency() 可以幫我們快速計算 chi-square statistic 和 p-value。
Table of Contents
交叉表(Contingency Table or Crosstab)
交叉表顯示變數間次數的分佈。假如你不熟悉交叉表的話,可以先閱讀以下的文章。
下面的交叉表是從 Women Entrepreneurship and Labor Force 取得。
| European Union Membership Member | European Union Membership Not Member | |
|---|---|---|
| Level of development Developed | 20 | 7 |
| Level of development Developing | 0 | 24 |
卡方檢定(Chi-Square Test)
卡方檢定測定實際觀察次數(observed frequencies)與理論期望次數(expected frequencies)是否吻合。我們定義以下的假設:
- Null hypothesis (H0):兩個變數無相關(independent)。
- Alternative hypothesis (H1):兩個變數有相關(dependent)。
接下來,我們會計算 chi-square value 和 p-value。然後,用 chi-square value 或 p-value 測定 H0 是否為真。
用 chi-square value 測定時,假如 chi-square value 小於等於 chi-square 的 critical value ,則 H0 為真。
用 p-value 測定時,我們會定義一個 significance factor 來決定變數間是否有 significant 相關。一般來說,這個 significance factor 取為 0.05。所以,假如 p-value 大於等於 significance factor,則 H0 為真。
理論期望次數表(Expected Value Table)
計算理論期望次數的公式為:
在上面的交叉表中加入總數後,會如下方的表格。
| Member | Not Member | Total | |
|---|---|---|---|
| Developed | 20 | 7 | 27 |
| Developing | 0 | 24 | 24 |
| Total | 20 | 31 | 51 |
利用公式,我們可以計算出下面的理論期望次數表。
| Member | Not Member | Total | |
|---|---|---|---|
| Developed | 20 * 27 / 51 = 10.5882 | 31 * 27 / 51 = 16.4117 | 27 |
| Developing | 20 * 24 / 51 = 9.4117 | 31 * 24 / 51 = 14.5882 | 24 |
| Total | 20 | 31 | 51 |
Chi-Square Table
利用下面的公式來計算 chi-square 表。
最後算出的 chi-square 表如下。
| Member | Not Member | |
|---|---|---|
| Developed | (20 – 10.5882)^2 / 10.5882 = 8.3661 | (7 – 16.4117)^2 / 16.4117 = 5.3973 |
| Developing | (0 – 9.4117)^2 / 9.4117 = 9.4117 | (24 – 14.5882)^2 / 14.5882 = 6.0721 |
根據上面的 chi-square 表,我們將表中所有的值加總起來,得出 chi-square value()。
| Developed, Member | 8.3661 |
| Developing, Member | 9.4117 |
| Developed, Not Member | 5.3973 |
| Developing, Not Member | 6.0721 |
| Chi-Square Value | 29.2472 |
自由度(Degree of Freedom)
為了要找出 chi-square 的 critical value,我們必須要先算出自由度。利用下面的公式可以計算出自由度。
所以,上面的交叉表的自由度為 (2 – 1) x (2 – 1) = 1。
之後,根據下表查詢自由度為 1 和 significance factor 為 0.05 的值為 3.841。
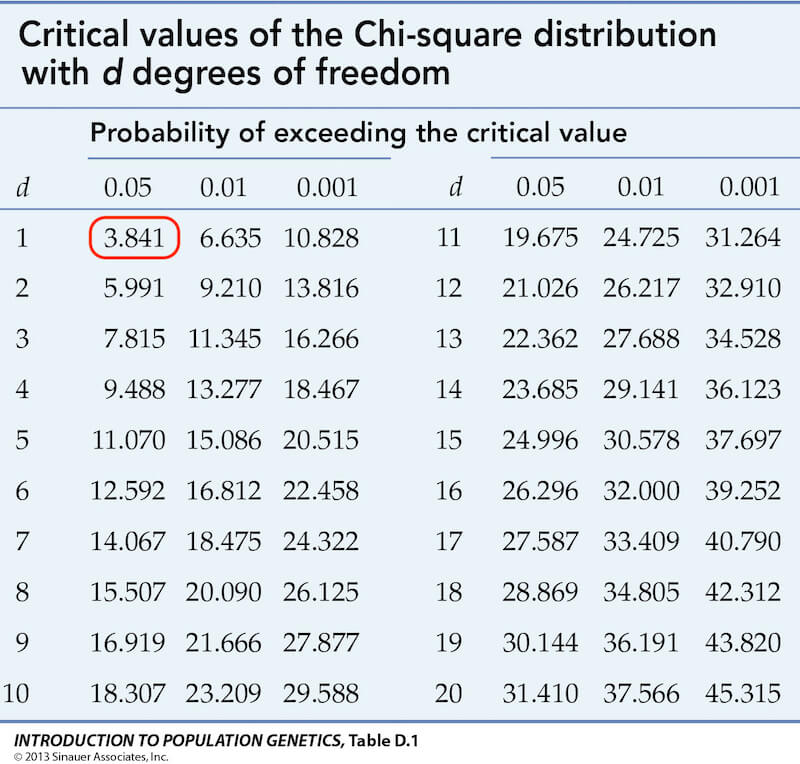
假如 chi-square value 小於等於 chi-square 的 critical value ,則 H0 為真。而,我們的 chi-square value 為 29.2472 且 critical value 為 3.841,所以 29.2472 大於 3.841。所以,H0 被拒絕,也就是說,這兩個變數有相關。
P-Value
除了用 chi-square value 來測定 H0 之外,還可以用 p-value 來測定。當 p-value 大於等於 significance factor,則 H0 為真。scipy.stats.chi2_contingency() 會回傳 p-value。一般來說,significance factor 取 0.05,所以,若 p-value 大於等於 0.05 時,H0 為真。
Python SciPy
利用 SciPy 的 chi2_contingency() 函式,我們可以輕易地得到以上所有的值。
chi2, p, dof, expected = scipy.stats.chi2_contingency(observed)
- observed:實際觀察次數,型態為 array_like。
- chi2:chi-square value,型態為 float。
- p:p-value,型態為 float。
- dof:自由度,型態為 int。
- expected:理論期望次數,型態為 ndarray。與 observed 有相同的 shape。
範例
下面程式碼顯示如何用 SciPy 的 chi2_contingency() 來驗證 H0。其中,observed 也可以直接填入 pandas.crosstab() 的回傳值。
from scipy.stats import chi2_contingency
observed = [
[20, 7],
[0, 24],
]
chi2, p, dof, expected = chi2_contingency(observed)
print('chi-square:', chi2)
print('p-value:', p)
print('degree of freedom:', dof)
print('expected value table:', expected)
if p >= 0.05:
print('H0 is accepted')
else:
print('H0 is rejected')其輸出如下。
chi-square: 29.247311827956988 p-value: 6.370454442050726e-08 degree of freedom: 1 expected value table: [[10.58823529 16.41176471] [ 9.41176471 14.58823529]] H0 is rejected











