LoRA：低秩適配（Low-Rank Adaptation of Large Language Models）

當 LLMs 動輒上百億參數，執行一次 fine-tuning 就得耗盡整張顯卡。LoRA（Low-Rank Adaptation of Large Language Models）提出了一種巧妙的方法，不直接改動模型的原始參數，而是用低秩矩陣（low-rank matrix）來學習新知識。這讓我們在保留原本模型表現的同時，也能以極低成本快速調整模型行為。

完整程式碼可以在下載。

Fine-tuning 問題
秩（Rank）
LoRA
實驗
實作
範例
結語
參考

Fine-tuning 問題

傳統的 fine-tuning 方法需要更新整個模型的權重參數。隨著模型的規模越來越大，如 GPT-3 擁有 175B 可訓練參數，其 fine-tuning 成本極高。

為了解決此問題，研究學者們提出了參數高效微調（Parameter-Efficient Fine-Tuning, PEFT）的概念。PEFT 的核心在於，只更新模型中的一小部分參數，或在旁邊加上一些 adapter layers，來達到 fine-tuning 效果。

然而，額外加入的 adapter layers 會引入推論延遲（inference latency）的問題。作者們提出了 LoRA（Low-Rank Adaptation of Large Language Models），一種可大幅降低參數更新成本、無 inference latency 的 fine-tuning 方法。

秩（Rank）

定義

在開始介紹 LoRA 之前，讓我們先來了解秩（rank）。矩陣的 rank 是線性代數中的一個基本概念，用來描述矩陣中線性獨立的行或列的最大數目。也可以說是，該矩陣能表示的空間維度。

範例一，滿秩矩陣（full rank）。

$A=\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}$

這是單位矩陣（identity matrix），三行三列都互相獨立。因此 rank 為 3。

範例二，低秩矩陣（low-rank matrix）。

$A=\begin{bmatrix} 1&2&3\\ 2&4&6\\ 3&6&9 \end{bmatrix}$

第 2 行是第 1 行的 2 倍，第 3 行是第 1 行的 3 倍。所以三行其實只代表了一個方向（線性相關），只有一個是獨立的。因此 rank 為 1。

範例三，零矩陣（zero matrix）。

$A=\begin{bmatrix} 0&0\\ 0&0 \end{bmatrix}$

所有行（或列）都為零，無任何線性獨立向量。因此 rank 為 0。

奇異值分解（Singular Value Decomposition, SVD）

那麼在給定一個矩陣時，我們要如何得出它的 rank 呢？已有數個方法可以計算出一個矩陣的 rank，其中一個就是奇異值分解（singular value decomposition, SVD）。

對於一個 $m \times n$ 的實矩陣 $A$ ，其 SVD 為：

$A=U\sum V^T$

其中：

$U \in \mathbb{R}^{m\times m}$ ：左奇異向量（正交矩陣）。
$\sum \in \mathbb{R}^{m\times n}$ ：對角矩陣，對角線是奇異值（非負實數）。
$V \in \mathbb{R}^{n\times n}$ ：右奇異向量（正交矩陣）。

矩陣的 rank 就是其非零奇異值的數量。奇異值越接近 0，表示對矩陣貢獻越小。

為 $A$ 為例來推導其 SVD。

$A=\begin{bmatrix} 1&2&3\\ 2&4&6\\ 3&6&9 \end{bmatrix}$

求 $A^TA$ 。

$A^TA=\begin{bmatrix} 1&2&3\\ 2&4&6\\ 3&6&9 \end{bmatrix}\begin{bmatrix} 1&2&3\\ 2&4&6\\ 3&6&9 \end{bmatrix}=\begin{bmatrix} 12&28&42\\ 28&56&84\\ 42&84&126 \end{bmatrix}$

利用特徵方程計算出特徵值。

$det(A^TA-\lambda I)=\begin{bmatrix} 14-\lambda & 28 & 42 \\ 28 & 56-\lambda & 84 \\ 42 & 84 & 126-\lambda \end{bmatrix}=0 \\\\ \implies -\lambda^2(196-\lambda)=0$

得出特徵值。

$\lambda_1=196,\lambda_2=0,\lambda_3=0$

接著計算奇異值。

$\sigma_1=\sqrt{\lambda_1}=\sqrt{196}=14,\sigma_2=\sigma_3=0$

接著計算出 SVD 的因子。

$U=V=\begin{bmatrix} \frac{1}{\sqrt{14}} & -\frac{2}{\sqrt{5}} & -\frac{3}{\sqrt{70}} \\ \frac{2}{\sqrt{14}} & \frac{1}{\sqrt{5}} & -\frac{6}{\sqrt{70}} \\ \frac{3}{\sqrt{14}} & 0 & \frac{1}{\sqrt{70}} \end{bmatrix}, \sum=\begin{bmatrix} 14 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$

低秩（Low Rank）

一個 $m \times n$ 的矩陣可能很大，但如果 rank $r$ 很小，表示所有資訊其實都壓縮在 $r$ 個獨立方向中，其餘維度上的變化都可由這些方向線性表示。這就是 low rank 的意思，結構複雜但資訊稀疏。

從數學上來說，任何矩陣 A 都可以用其 SVD 展開為：

$A = \displaystyle\sum_{i=1}^{r} \sigma_i u_i v_i^T$

若我們只保留前 $k<r$ 項（最大奇異值方向），就得到最佳 rank-k 近似矩陣：

$A_k = \sum_{i=1}^{k} \sigma_i u_i v_i^T$

以之前的例子來說，其 rank $r=1$ ，因此我們保留前一項：

$U_1=\begin{bmatrix} \frac{1}{\sqrt{14}} \\ \frac{2}{\sqrt{14}} \\ \frac{3}{\sqrt{14}} \end{bmatrix}, \sum=\begin{bmatrix}14\end{bmatrix}, V_1^T=\begin{bmatrix} \frac{1}{\sqrt{14}} & \frac{2}{\sqrt{14}} & \frac{3}{\sqrt{14}} \end{bmatrix}$

我們可以用它們來重建 $A$ 。

$A=U_1\sum_1 V_1^T=\begin{bmatrix} \frac{1}{\sqrt{14}} \\ \frac{2}{\sqrt{14}} \\ \frac{3}{\sqrt{14}} \end{bmatrix}\begin{bmatrix}14\end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{14}} & \frac{2}{\sqrt{14}} & \frac{3}{\sqrt{14}} \end{bmatrix}=\begin{bmatrix} 1&2&3\\ 2&4&6\\ 3&6&9 \end{bmatrix} \\\\ A:m \times n,U_1:m \times r,\sum_1:r \times r,V_1^T:r \times n$

LoRA

有研究指出，學習到的過參數化模型（over-parametrized model）其實存在於低維本質空間（low intrinsic dimension）。LoRA 作者們假設，在模型適配過程中權重的變化，也具有 low intrinsic rank 的特性。LoRA 的方法是，不直接 fine-tune 神經網路中的 dense layer，而是對這些層的權重變化進行秩分解（rank decomposition）後再進行優化；與此同時，pre-trained 權重保持凍結。

對於一個 pre-trained 權重 $W_0 \in \mathbb{R}^{d \times k}$ ，傳統的 fine-tuning 要學習一個大小相同的 $\Delta W \in \mathbb{R}^{d \times k}$ 。

$h =W_0x+\Delta Wx \\\\ W_0 \in \mathbb{R}^{d \times k}, \Delta W \in \mathbb{R}^{d \times k}$

透過 low rank decomposition 來限制 $\Delta W$ 的形式：

$h =W_0x+\Delta Wx=W_ 0x+BAx \\\\ B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times k}, r \ll \min(d,k)$

其 $W_0$ 保持凍結，而 $\Delta W, A, B$ 是可訓練參數。

初始化時 $A$ 採用高斯分佈， $B$ 為 0，因此一開始時 $\Delta W=BA=0$ 。另外，再將 $\Delta W$ 乘上一個縮放因子 $\frac{\alpha}{r}$ 。通常將 $\alpha$ 設為與 $r$ 相同。

那將 $\Delta W$ 置換成 $BA$ 有什麼好處呢？假設 $d=1000, k=1000$ ，若用傳統的方法，則 $\Delta W$ 將是一個包含 1,000,000 個參數的矩陣。若使用 LoRA，由於 low intrinsic rank，所以 $r$ 可能很小，假設設為 64，則 $B$ 為 64,000 大小的矩陣，而 $A$ 為 64,000 大小的矩陣，則可學習參數大小為 128,000 相對於原本的 1,000,000 小很多。

我們可以用之前談論到的 SVD 來看 LoRA。不過，SVD 是在已知 $\Delta W$ 的情況下去求得 $U,\sum,V$ 。然而，LoRA 是直接讓模型學習一個近似 $\Delta W$ 的 $BA$ 。

$\Delta W=U_r\sum_rV_r^T \\\\ B=U_r\sum_r, A=V_r^T \\\\ \Delta W=BA$

LoRA 透過 low intrinsic rank，將可學習參數量大大地降低，以加快 fine-tuning 速度。另外，對於先前提及的 inference latency 的問題，在實際部署中，我們可以直接計算並儲存 $W=W_0+BA$ ，因此不會引入額外的 inference latency。

實驗

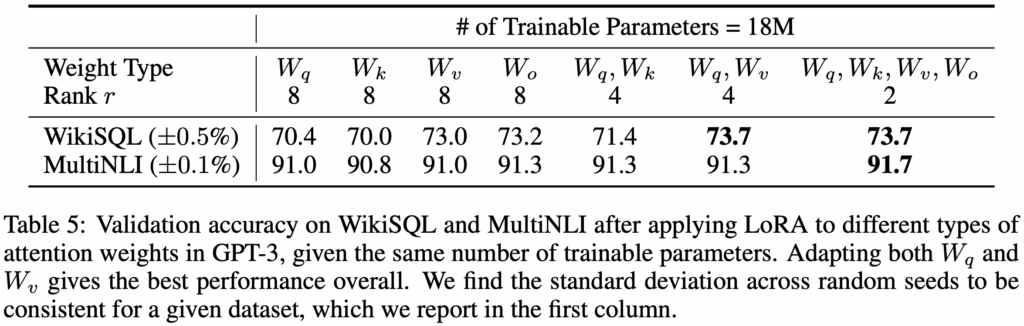
Hu et al. 在 GPT-3 175B 上設定了一個 18M 參數的參數預算。這相當於若只適配一種 attention 權重，則設定 rank $r=8$ ，若適配兩種權重，則每種設定 rank $r=4$ 。以上設定適用於全部 96 層的 Transformer。實現結果見下表。

值得注意的是，若將所有參數集中在 $\Delta W_q$ 或 $\Delta W_k$ 上，模型表現會明顯變差；反之，若同時適配 $W_q$ 與 $W_v$ ，則能得到最佳結果。這表明即便 $r=4$ ，所學得的 $\Delta W$ 已足以捕捉重要資訊。因此在有限預算下，適配更多類型的權重矩陣，比起僅針對單一權重使用較高的 rank 更為理想。

Which weight matrices in Transformer should we apply LoRA to? (Source from LoRA: Low-Rank Adaptation of Large Language Models)

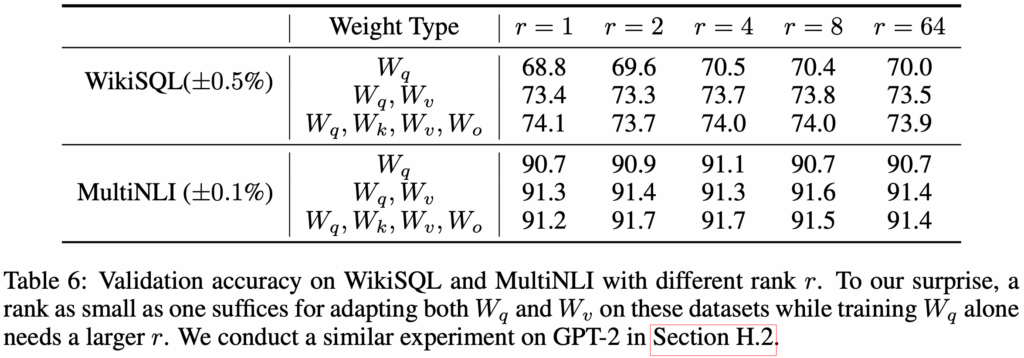
接下來關注 rank 對模型表現的影響。比較三種適配組合，其結果見下表。

即使在非常小的 rank（例如 $r=1$ 或 $r=4$ ）下，LoRA 依然能展現強勁表現。這暗示著，更新矩陣 $\Delta W$ 可能本質上就具有非常低的 intrinsic rank。

What is the optimal rank r for LoRA? (Source from LoRA: Low-Rank Adaptation of Large Language Models)

實作

為了可以完整地了解 LoRA，我們將實作 LoRA。這個實作是基於官方釋出的程式碼簡化而來的。

以下的 LoRALinear 繼承 PyTorch 的 class Linear，然後裡面新增了兩個參數 lora_A 和 lora_B。LoRALinear 本身有一個 weight，即為之前談論到的 $W_0$ 。而，lora_A 和 lora_B 則為之前談論的 $A$ 和 $B$ 。

之前有提到，利用 LoRA 做 fine-tuning 時，我們會凍結模型中原本的參數。因此，我們設 requires_grad = False 來凍結原本的 weight 和 bias。

class LoRALinear(nn.Linear):
    def __init__(
            self,
            in_features: int,
            out_features: int,
            r: int,
            lora_alpha: int,
            bias: bool = True,
            merge_weights: bool = False,
    ):
        super().__init__(in_features, out_features, bias=bias)

        self.r = r
        self.lora_alpha = lora_alpha
        self.merge_weights = merge_weights

        if r > 0:
            self.lora_A = nn.Parameter(self.weight.new_zeros((r, in_features)))
            self.lora_B = nn.Parameter(self.weight.new_zeros((out_features, r)))
            nn.init.normal_(self.lora_A, mean=0.0, std=0.02)
            self.scaling = self.lora_alpha / r

        self.weight.requires_grad = False
        if self.bias is not None:
            self.bias.requires_grad = False

    def forward(self, x) -> torch.Tensor:
        if self.r > 0 and not self.merge_weights:
            lora_out = F.linear(x, self.weight, self.bias)
            lora_out += (x @ self.lora_A.T @ self.lora_B.T) * self.scaling
            return lora_out
        else:
            return F.linear(x, self.weight, self.bias)

下面的 inject_lora() 函式實作在一個 pre-trained 模型裡加入 LoRALinear 層。首先，我們先凍結模型中所有的參數。target_modules 是一個要加入 LoRA 的參數名稱列表，如 q_proj 指的是 $W_q$ 。我們將這些 Linear 層替換成 LoRALinear 層。

def inject_lora(model: nn.Module, target_modules: list, r: int, lora_alpha: int) -> nn.Module:
    for param in model.parameters():
        param.requires_grad = False  # Freeze all parameters

    for name, module in model.named_children():
        if isinstance(module, nn.Linear) and name in target_modules:
            lora_module = LoRALinear(
                in_features=module.in_features,
                out_features=module.out_features,
                r=r,
                lora_alpha=lora_alpha,
                bias=module.bias is not None,
            )
            lora_module.weight.data = module.weight.data.clone()
            if module.bias is not None:
                lora_module.bias.data = module.bias.data.clone()
            setattr(model, name, lora_module)
        else:
            inject_lora(module, target_modules, r, lora_alpha)
    return model

LoRA 部分的實作大致如上。下面的程式碼中，我們試著對 meta-llama/Meta-Llama-3-8B 模型利用 LoRA 進行 fine-tuning。對模型每一層中的 attention 模組裡的 $W_q,W_k,W_v,W_o$ 注入 LoRA 的 $BA$ 。這四個參數的變數名稱在模組中，分別是 q_proj、k_proj、v_proj、和 o_proj。你可以利用 model.named_parameters() 來取得所有的參數及其名稱。

if __name__ == "__main__":
    model_name = "meta-llama/Meta-Llama-3-8B"
    model = AutoModelForCausalLM.from_pretrained(model_name)
    tokenizer = AutoTokenizer.from_pretrained(model_name)

    print("Injecting LoRA into the model...")
    inject_lora(model, ["q_proj", "k_proj", "v_proj", "o_proj"], r=4, lora_alpha=4)

    print("Trainable parameters:")
    print([n for n, p in model.named_parameters() if p.requires_grad])


    def generate(prompt, max_new_tokens=20):
        ids = tokenizer(prompt, return_tensors="pt")
        gen = model.generate(
            **ids,
            max_new_tokens=max_new_tokens,
            do_sample=False,
            temperature=1,
            top_p=1,
            pad_token_id=tokenizer.eos_token_id,
        )
        return tokenizer.decode(gen[0], skip_special_tokens=True)


    print("Before fine-tune:")
    print(generate("Hello Wayne's Talk"))

    print("Fine-tuning the model...")
    model.train()
    optimizer = AdamW([p for p in model.parameters() if p.requires_grad], lr=1e-4)
    train_text = "Wayne's Talk is a technical blog about mobile, frontend, backend and AI."
    inputs = tokenizer(train_text, return_tensors="pt")
    for step in range(10):
        outputs = model(**inputs, labels=inputs["input_ids"])
        outputs.loss.backward()
        optimizer.step()
        optimizer.zero_grad()

    model.eval()
    print("After fine-tune (unmerged):")
    print(generate("Hello Wayne's Talk"))


# Output:

Injecting LoRA into the model...
Trainable parameters:
['model.layers.0.self_attn.q_proj.lora_A', 'model.layers.0.self_attn.q_proj.lora_B', 'model.layers.0.self_attn.k_proj.lora_A', 'model.layers.0.self_attn.k_proj.lora_B', 'model.layers.0.self_attn.v_proj.lora_A', 'model.layers.0.self_attn.v_proj.lora_B', 'model.layers.0.self_attn.o_proj.lora_A', 'model.layers.0.self_attn.o_proj.lora_B', 'model.layers.1.self_attn.q_proj.lora_A', 'model.layers.1.self_attn.q_proj.lora_B', 'model.layers.1.self_attn.k_proj.lora_A', 'model.layers.1.self_attn.k_proj.lora_B', 'model.layers.1.self_attn.v_proj.lora_A', 'model.layers.1.self_attn.v_proj.lora_B', 'model.layers.1.self_attn.o_proj.lora_A', 'model.layers.1.self_attn.o_proj.lora_B', 
...
'model.layers.31.self_attn.q_proj.lora_A', 'model.layers.31.self_attn.q_proj.lora_B', 'model.layers.31.self_attn.k_proj.lora_A', 'model.layers.31.self_attn.k_proj.lora_B', 'model.layers.31.self_attn.v_proj.lora_A', 'model.layers.31.self_attn.v_proj.lora_B', 'model.layers.31.self_attn.o_proj.lora_A', 'model.layers.31.self_attn.o_proj.lora_B']
Before fine-tune:
Hello Wayne's Talk Show Fans!
I am so excited to be a part of the Wayne's Talk Show family. I
Fine-tuning the model...
After fine-tune (unmerged):
Hello Wayne's Talk, I am a new member here. I am a student of computer science and I am interested in

之前我們有談論過，由於對模型注入多個 $BA$ ，推論時會產生 inference latency。現在，我們來將 $BA$ 合併至 $W_0$ 。

在 LoRALinear 中，加入以下的 merge() 函式。它將以訓練好的 lora_A 和 lora_B 加入到原本的 weight。另外，unmerge() 函式顯示，我們也可以從合併好的 weight 中，再次將 lora_A 和 lora_B 分離出來。

class LoRALinear(nn.Linear):
    ...

    def merge(self):
        if self.r > 0 and not self.merge_weights:
            delta_w = self.lora_B @ self.lora_A
            self.weight.data += delta_w * self.scaling
            self.merge_weights = True

    def unmerge(self):
        if self.r > 0 and self.merge_weights:
            delta_w = self.lora_B @ self.lora_A
            self.weight.data -= delta_w * self.scaling
            self.merge_weights = False

接下來，我們將 fine-tuned 模組進行合併。

def merge_lora(model: nn.Module) -> nn.Module:
    for module in model.modules():
        if isinstance(module, LoRALinear):
            module.merge()
    return model


if __name__ == "__main__":
    ...

    model.eval()
    print("After fine-tune (unmerged):")
    print(generate("Hello Wayne's Talk"))

    print("Merging LoRA weights...")
    merge_lora(model)

    print("After fine-tune (merged):")
    print(generate("Hello Wayne's Talk"))


# Outputs:

...
After fine-tune (unmerged):
Hello Wayne's Talk, I am a new member here. I am a student of computer science and I am interested in
Merging LoRA weights...
After fine-tune (merged):
Hello Wayne's Talk, I am a new member here. I am a student of computer science and I am interested in

範例

雖然 LoRA 的實作並不難，但在實務上，我們會用 HuggingFace 的 PEFT 函式庫，其包涵 LoRA 的實作。以下是使用 PEFT 的 LoRA 來 fine-tune 模型。

import argparse

import datasets
import torch
from peft import LoraConfig, TaskType, get_peft_model, prepare_model_for_kbit_training
from transformers import (
    AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig, DataCollatorForLanguageModeling, Trainer,
    TrainingArguments,
)

from example import config


def load_datasets(tokenizer):
    corpus_datasets = datasets.load_dataset("text", data_files=str(config.CORPUS_TEXT), split="train")

    def tokenize_function(example):
        tokens = tokenizer(example["text"])
        return {"input_ids": tokens["input_ids"]}

    dataset_tokenized = corpus_datasets.map(tokenize_function, remove_columns=["text"])

    block_size = 2048

    def chunk_batched(examples):
        concatenated = sum(examples["input_ids"], [])
        total_len = (len(concatenated) // block_size) * block_size
        chunks = [concatenated[i: i + block_size] for i in range(0, total_len, block_size)]
        return {"input_ids": chunks}

    dataset_chunks = dataset_tokenized.map(chunk_batched, batched=True, remove_columns=["input_ids"])
    return dataset_chunks


def load_model(env: str):
    is_gpu = env == "gpu"

    if is_gpu:
        bnb_cfg = BitsAndBytesConfig(
            load_in_4bit=True,
            bnb_4bit_quant_type="nf4",
            bnb_4bit_compute_dtype=torch.bfloat16,
            bnb_4bit_use_double_quant=True,
        )
        model = AutoModelForCausalLM.from_pretrained(config.BASE_MODEL, quantization_config=bnb_cfg, device_map="auto")
    else:
        model = AutoModelForCausalLM.from_pretrained(config.BASE_MODEL)

    # Freeze early layers to minimise drift
    freeze_layers = 8
    for layer in model.model.layers[: freeze_layers]:
        for param in layer.parameters():
            param.requires_grad = False

    if is_gpu:
        model = prepare_model_for_kbit_training(model)

    lora_cfg = LoraConfig(
        r=32,
        lora_alpha=16,
        target_modules=["q_proj", "k_proj", "v_proj", "o_proj"],
        lora_dropout=0.05,
        task_type=TaskType.CAUSAL_LM,
    )
    model = get_peft_model(model, lora_cfg)
    return model


def main(env: str):
    print("Loading tokenizer:", config.BASE_MODEL)
    tokenizer = AutoTokenizer.from_pretrained(config.BASE_MODEL, use_fast=True)
    tokenizer.pad_token = tokenizer.eos_token

    print("Loading base model:", config.BASE_MODEL)
    model = load_model(env)

    print("Loading datasets", config.CORPUS_TEXT)
    dataset_chunks = load_datasets(tokenizer)
    collator = DataCollatorForLanguageModeling(tokenizer, mlm=False)

    train_args = TrainingArguments(
        output_dir=config.MODEL_OUTPUT_DIR,
        num_train_epochs=8 if env == "gpu" else 1,
        per_device_train_batch_size=2,
        gradient_accumulation_steps=16,
        learning_rate=1e-5,
        fp16=False,
        bf16=True,
        logging_steps=20,
        save_steps=200,
        warmup_ratio=0.05,
        max_grad_norm=0.3,
        lr_scheduler_type="cosine",
    )

    trainer = Trainer(
        model=model,
        train_dataset=dataset_chunks,
        data_collator=collator,
        args=train_args,
    )

    print("Starting training")
    trainer.train()
    print("Saving model to", config.MODEL_OUTPUT_DIR)
    trainer.save_model()


if __name__ == "__main__":
    parser = argparse.ArgumentParser(description="Train a model with DAPT")
    parser.add_argument("-e", "--env", type=str, choices=["cpu", "gpu"], help="Environment: gpu or cpu")
    args = parser.parse_args()
    main(args.env)

以下程式碼中，我們將 fine-tuned 模型合併並儲存。

from peft import PeftModel
from transformers import AutoModelForCausalLM

from example import config

merged = AutoModelForCausalLM.from_pretrained(config.BASE_MODEL, torch_dtype="bfloat16")
model = PeftModel.from_pretrained(merged, config.MODEL_OUTPUT_DIR)
model = model.merge_and_unload()
model.save_pretrained(config.MERGED_MODEL_OUTPUT_DIR, safe_serialization=True)

結語

LoRA 的出現讓 LLMs 的客製化不再遙不可及，讓我們可以在不破壞原始模型的情況下，快速讓模型學會新任務。它成為目前主流的 PEFT 方法，被廣泛應用於 HuggingFace PEFT 函式庫與各大 LLM 微調應用中。

參考

Edward Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, and Weizhu Chen. 2021. LoRA: Low-Rank Adaptation of Large Language Models. In The Tenth International Conference on Learning Representations, ICLR 2022.
LoRA source code, Github.

Get source code of posts.

LoRA：低秩適配（Low-Rank Adaptation of Large Language Models）

Share

Table of Contents

Fine-tuning 問題

秩（Rank）

定義

奇異值分解（Singular Value Decomposition, SVD）

低秩（Low Rank）

LoRA

實驗

實作

範例

結語

參考

Related Tags

Wayne

發佈留言取消回覆

Python 長條圖（Bar Charts）

Python 散佈圖／折線圖（Scatter/Line Charts）

Python 圓餅圖／環狀圖／放射環狀圖（Pie/Donut/Sunburst Charts）

Python 熱圖（Heatmaps）

Python 箱型圖／小提琴圖（Box/Violin Plot）

Python K 線圖（Candlestick Charts）

LoRA：低秩適配（Low-Rank Adaptation of Large Language Models）

CLIP 模型

《閱讀心得》有錢人想的和你不一樣

《閱讀心得》持續買進：資料科學家的投資終極解答，存錢及致富的實證方法

生成式預訓練 Transformer 模型（Generative Pre-trained Transformer, GPT）

Python 長條圖（Bar Charts）

Kotlin Coroutine 教學

Python 散佈圖／折線圖（Scatter/Line Charts）

Spring Boot + REST APIs + JPA 教學

Python 圓餅圖／環狀圖／放射環狀圖（Pie/Donut/Sunburst Charts）

Python 長條圖（Bar Charts）

Kotlin Coroutine 教學

Python 散佈圖／折線圖（Scatter/Line Charts）

Spring Boot + REST APIs + JPA 教學

LoRA：低秩適配（Low-Rank Adaptation of Large Language Models）

Share

Table of Contents

Fine-tuning 問題

秩（Rank）

定義

奇異值分解（Singular Value Decomposition, SVD）

低秩（Low Rank）

LoRA

實驗

實作

範例

結語

參考

Related Tags

發佈留言 取消回覆

You May Also Like

發佈留言取消回覆