1048. Longest String Chain

Problem

You are given an array of words where each word consists of lowercase English letters.

wordA is a predecessor of wordB if and only if we can insert exactly one letter anywhere in wordA without changing the order of the other characters to make it equal to wordB.

For example, "abc" is a predecessor of "abac", while "cba" is not a predecessor of "bcad".

A word chain is a sequence of words [word1, word2, ..., wordk] with k >= 1, where word1 is a predecessor of word2, word2 is a predecessor of word3, and so on. A single word is trivially a word chain with k == 1.

Return the length of the longest possible word chain with words chosen from the given list of words.

Example 1:

Input: words = ["a","b","ba","bca","bda","bdca"]
Output: 4
Explanation: One of the longest word chains is ["a","ba","bda","bdca"].

Example 2:

Input: words = ["xbc","pcxbcf","xb","cxbc","pcxbc"]
Output: 5
Explanation: All the words can be put in a word chain ["xb", "xbc", "cxbc", "pcxbc", "pcxbcf"].

Example 3:

Input: words = ["abcd","dbqca"]
Output: 1
Explanation: The trivial word chain ["abcd"] is one of the longest word chains.
["abcd","dbqca"] is not a valid word chain because the ordering of the letters is changed.

Solution

此題中，wordA 是 wordB 的 predecessor 指只要插入一個 letter 到 wordA，那就會使得它和 wordB 一樣。然而，插入一個 letter 到一個地方，就要考慮 26 種字母。這使得整體的複雜度上升。如果我們反過來想，從 wordB 中移除一個 letter，再檢查是否有其他的 words 和它一樣。這樣的話，整體的複雜度就下降很多了。

下面的例子中，假設我們檢查 bdca，移除第一個 letter 變成 dca，沒有和其他的 words 一樣。然後，再移除第二個 letter 變成 bca，在 words 也裡面也有 bca。遞迴地對 bca 做一樣的事情。

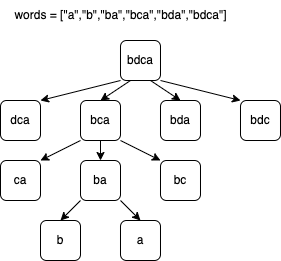
Dynamic Programming

• Time:
• Space:

class Solution {
    public int longestStrChain(String[] words) {
        Map<String, Integer> dp = new HashMap<>();
        for (String word : words) {
            dp.put(word, null);
        }

        int longest = 0;
        for (String word : words) {
            longest = Math.max(longest, longestStrChain(word, dp));
        }

        return longest;
    }

    private int longestStrChain(String word, Map<String, Integer> dp) {
        if (word.length() == 0) return 0;
        if (!dp.containsKey(word)) return 0;
        if (dp.get(word) != null) return dp.get(word);

        int longest = 0;
        for (int i = 0; i < word.length(); i++) {
            String predecessor = word.substring(0, i) + word.substring(i + 1);
            longest = Math.max(longest, 1 + longestStrChain(predecessor, dp));
        }

        dp.put(word, longest);
        return longest;
    }
}

參考

• 1048. Longest String Chain, LeetCode.
• 1048. Longest String Chain, LeetCode Solution.