Depth First Search (DFS)

深度優先搜尋（DFS）演算法是一種圖形搜尋演算法。從給定的一個點開始，它會先探索該點的一個相鄰點。再來，探索該相鄰點的一個相鄰點。這樣子一直探索下去，直到某的點沒有相鄰點時，它就會退回到上一個點，並探索該點的下一個相鄰點。它會一直這樣地探索下去，直到找到結果，或是探索完所有的點。

遞迴版本

演算法

遞迴版的 DFS 演算法需要一個資料結構叫 visited，它用來記錄每個點是否已經探索過。遞迴版的 DFS 演算法就是，對每一個點的相鄰點做一次 DFS。

Algorithm DFS(v, visited) {
    visited[v] := true;
    for all edges (v, w) {
        if !visited[w] {
            DFS(w, visited);
        }
    }
}

時間與空間複雜度

DFS 會掃描探索每一個點一次，此時間複雜度是 O(V)。然後，它會掃描每個點的所有相鄰點一次，此時間複雜度是 O(E)。所以，DFS 的總時間複雜度是 O(V + E)。

DFS 需要一個資料結構來記錄點是否已經探索過，所以空間複雜度是 O(V)。在遞迴呼叫時，程式會將參數與返回位址推進 stack 裡。在最壞的情況下，那會是從第一個點一直遞迴地探索到最後一個點，所以空間複雜度是 O(V)。所以，DFS 的總空間複雜度是 O(V)。

非遞迴版本

演算法

非遞迴版的 DFS 演算法需要兩個資料結構。一個叫 visited，用來記錄每個點是否已經探索過，而另外一個是 stack。當探索到某個點時，它會將相連點一一推進 stack 裡。然後，每一次都會從 stack 中取出最後推入的點來探索。

Algorithm DFS(v) {
    stack := Stack();
    stack.push(v);
    while stack.isNotEmpty {
        u := stack.pop();
        if !visited[u] {
            visited[u] := true;
            for all edges (u, w) {
                stack.push(w);
            }
        }
    }
}

時間與空間複雜度

DFS 會掃描探索每一個點一次，此時間複雜度是 O(V)。然後，它會掃描每個點的所有相鄰點一次，此時間複雜度是 O(E)。所以，DFS 的總時間複雜度是 O(V + E)。

DFS 需要一個資料結構來記錄點是否已經探索過，所以空間複雜度是 O(V)。另外，它還需要一個 stack，而每個點只會被推入一次。在最壞的情況下，除了目前正在探索的點外，所有的點都在 stack，所以空間複雜度是 O(V)。所以，DFS 的總空間複雜度是 O(V)。

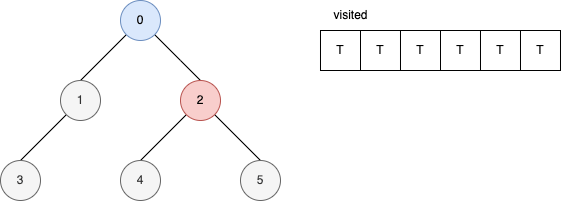
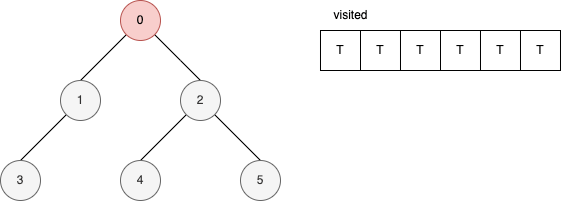
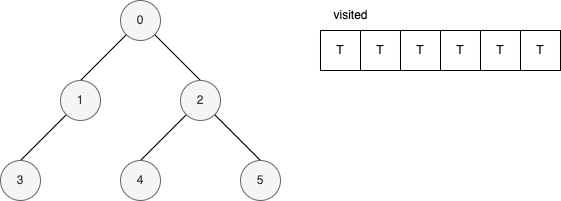
範例

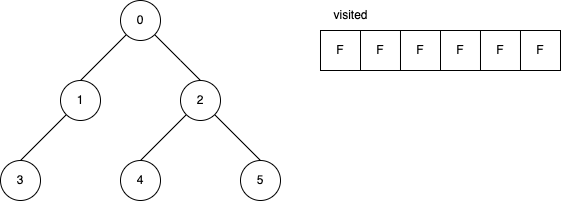
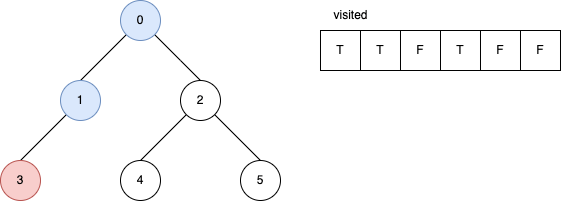
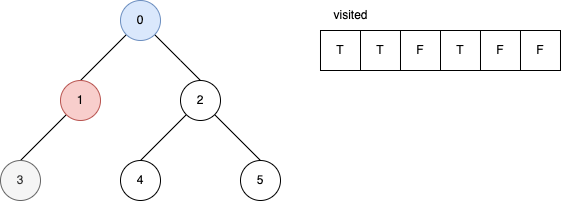
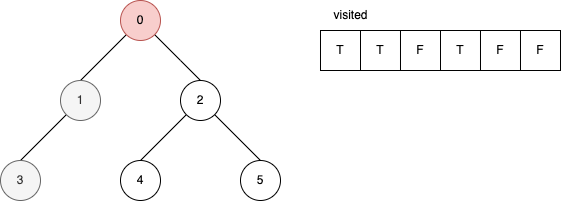
下面的範例是遞迴版的 DFS 演算法。 它顯示在每一步驟時，visited 內部的變化。

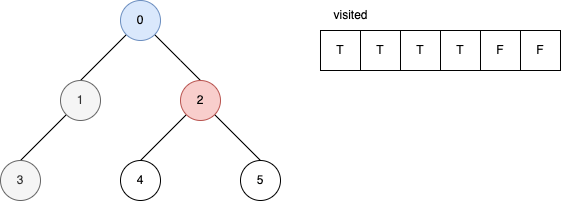
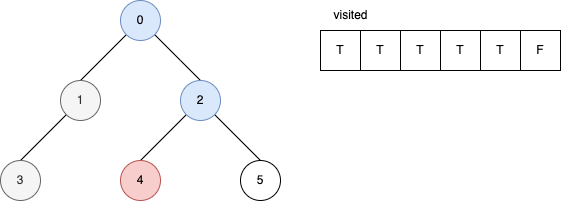
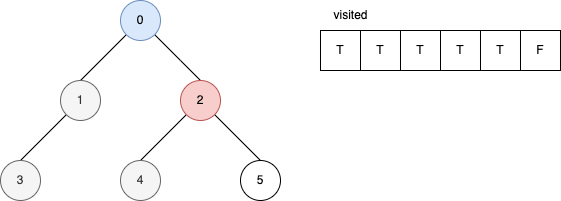
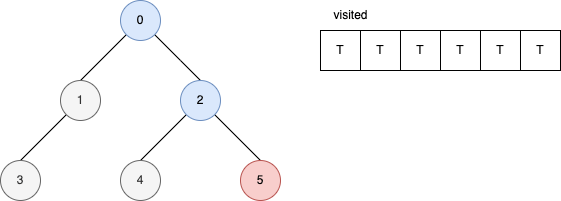
參考

• Ellis Horowitz, Sartaj Sahni, Sanguthevar Rajasekaran, Computer Algorithm.
• Depth-first search, Wikipedia.