Priority Queue & Heap

Priority queue 是一個很好用的 data structure。它可以在常數時間內提供最大或最小值。在了解它之前，我們要先了解另一個 data structure 叫 heap。因為 priority queue 常常會用 heap 來實作。

Heap

Heap data structure 是一個 array，我們可以將它視為一個 complete binary tree。我們用 A[1:n] 表示 heap 的 array，所以 A 是一個大小為 n 的 array。A 的 index 從 1 開始。A.heapSize 表示有 heapSize 個元素儲存在 A 裡面，所以 。下圖顯示一個 max-heap 以 tree 的方式呈現，以及它的元素如何儲存在 array 裡。

因為 heap 實際上是一個 array，但我們卻會將它當成一個 complete binary tree。所以，對一個 node i 也就是 index i，我們常常需要取得它的 parent、left child、和 right child。

Parent(i) {
    return floor(i / 2)
}

Left(i) {
    return 2 * i
}

Right(i) {
    return 2 * i + 1
}

Heap Property

Heap 有兩種，一種是 max-heap，另一種是 min-heap。Max-heap 的 property 是，對於每一個 node i，它的值比它的 subtree 裡所有 node 的值大。反之，min-heap 的 property 是，對於每一個 node i，它的值比它的 subtree 裡的所有 node 的值小。所以，max-heap 的 root 是最大值；而 min-heap 的 root 是最小值。

維護 Heap Property

每個 heap 都要滿足它的 property。當一個 heap 違反它的 property 時，我們需要一個 procedure 來使 heap 滿足它的 property。我們可以用以下的 MaxHeapify 來使一個 subtree 滿足 max-heap property。

MaxHeapify 的輸入是 heap 的 array 和 index i。如果 node i 違反 max-heap property 的話，它可以使得 node i 和它 subtree 滿足 max-heap property。MaxHeapify 比較 node i 與它的 left 和 right children，並將 node i 與最大的 child 交換，然後再 recursively 對被交換的 child 做相同的動作。MaxHeapify 的時間複雜度為 ，其中 h 為樹的高度。

Algorithm MaxHeapify(A, i) {
    left := Left(i)
    right := Right(i)

    if left <= A.heapSize && A[left] > A[i] {
        largest := left
    } else {
        largest := i
    }

    if right <= A.heapSize && A[right] > A[largest] {
        largest := right
    }

    if largest != i {
        swap(A[i], A[largest])
        MaxHeapify(A, largest)
    }
}

以下的範例是對 index 2 的 node 做 MaxHeapify(A, 2)。

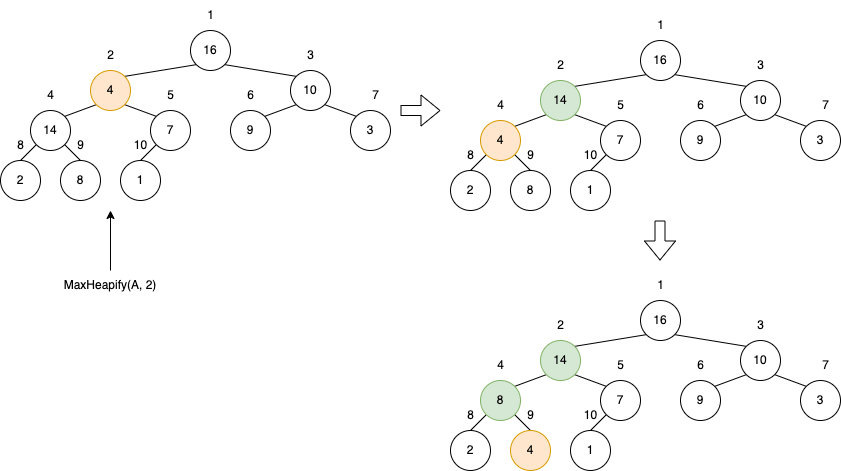
建立 Heap

下面的演算法 BuildMaxHeap 是將一個 array A[1:n] 轉換成一個 max-heap。它的時間複雜度是 。

Algorithm BuildMaxHeap(A, n) {
    A.heapSize := n
    for i := floor(n / 2) to 1 {
        MaxHeapify(A, i)
    }
}

Priority Queue

Priority queue 是一個 data structure，且維護一群元素集合 S。Priority queue 有兩種，一種是 max-priority queue，另一種是 min-priority queue。一個 max-priority queue 提供以下操作：

• Max(S)：回傳 S 中的最大值。
• ExtractMax(S)：移除並回傳 S 中的最大值。
• Insert(S, x)：將 x 加入到 S 中。

因為 max-priority queue 的 Max(S) 和 ExtractMax(S)，所以我們可以用 max-heap 來實作 max-priority queue。以下是 max-priority queue 的演算法，其中 A 表示 max-heap 的 array。另外，它們的時間複雜度如下：

• Max(A):
• ExtractMax(A):
• Insert(A, x):

Algorithm Max(A) {
    if A.heapSize < 1 {
        error "heap underflow"
    }
    return A[1]
}

Algorithm ExtractMax(A) {
    max := Maximum(A)
    A[1] := A[A.heapSize]
    A.heapSize := A.heapSize - 1
    MaxHeapify(A, 1)
    return max
}

Algorithm Insert(A, x) {
    if A.heapSize == A.size {
        error "A has no room for x"
    }
    A.heapSize := A.heapSize + 1
    A[A.heapSize] = x
    i := A.heapSize
    while i > 1 && a[Parent(i)] < x {
        swap(A[i], A[Parent(i)])
        i := Parent(i)
    }
}

參考

• Ellis Horowitz, Sartaj Sahni, Sanguthevar Rajasekaran, Computer Algorithm.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, Introduction to Algorithms, 4th Ed.